Answer:
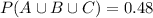
Explanation:
Given the following probabilities for events A and B
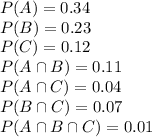
We want to find P(A ∪ B ∪ C).
Using the inclusion/exclusion formula for the union of three events:
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) − P(A ∩ B) − P(A ∩ C)−P(B∩C)+P(A∩B∩C).
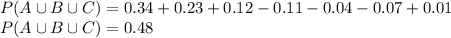
Therefore, P(A or B or C) = 0.48