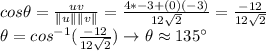Question

Consider the vectors Bold uuequals=left angle 4 comma 0 right angle4,0 and Bold vvequals=left angle negative 3 comma negative 3 right angle−3,−3. Sketch the​ vectors, find the angle between the​ vectors, and compute the dot product using the definition Bold u times Bold v equals StartAbsoluteValue Bold u EndAbsoluteValue StartAbsoluteValue Bold v EndAbsoluteValue cosine thetau•v=u vcosθ.

Answer 1

Check the graph below for the sketch.

`\theta=135^(\circ)`

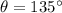
Explanation:

1) Let's organize the data from these Latex codes.

`\vec{\mathbf{u}}=\left \langle 4,0 \right \rangle\:and\: \vec{\mathbf{v}}=\left \langle -3,-3 \right \rangle`

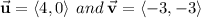
2) Sketching them (Check below). Notice that we are going to use the coordinates of each vector.

3) To find the angle between the vectors, we need to remember the Theorem:

If there is an angle between two vectors a and b, then we can calculate its angle using this relation:

`a*b=\left \| a \right \|\left \| b \right \|*cos\theta`

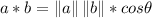
3.1) Then we need the Dot product between u and v. The Dot product is going to give us a scalar value for a product between vectors.

We will also need the norm of each vector. The norm will tell us the length of each one.

`\vec{u}*\vec{v}=\vec{u}*\vec{v}=4(-3)+0(-3)=-12\\\left \| u \right \|=√(4^2+0^2 )= \left \| u \right \|=4, \\\left \| v \right \|=√((-3)^2+(-3)^2), \left \| v \right \|=18=3√(2) \left\\`

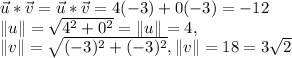
3.2)

Now, we can plug these pieces of information from 3.1 and 3.2 and find the angle:

`cos\theta=(uv)/(\left \| u \right \|\left \| v \right \|)=(4*-3+(0)(-3))/(12√(2) )=(-12)/( 12√(2) )\\\theta=cos^(-1)((-12)/( 12√(2) ))\rightarrow \theta\approx 135^(\circ)`

Answer 2

Angle between the two vectors is 135°

u•v = -12

Explanation:

Given two vectors u = (4,0) and v = (-3,-3).

To find the angle between the two vectors we will use the formula for calculating the angle between two vectors as shown;

u•v = |u||v|cos theta

cos theta = u•v/|u||v|

theta = arccos (u•v/|u||v|)

u•v = (4,0)•(-3,-3)

u•v = 4(-3)+0(-3)

u•v = -12

For |u| and |v|

|u| = √4²+0²

|u| = √16 = 4

|v| = √(-3)²+(-3)²

|v| = √9+9

|v| = √18

|v| = 3√2

|u||v| = 4×3√2 = 12√2

theta = arccos(-12/12√2)

theta = arccos(- 1/√2)

theta = -45°

Since cos is negative in the second quadrant, theta = 180-45°

theta = 135°

To get u•v using the formula u•v = |u||v|cos theta

Given |u||v| = 12√2 and theta = 135°

u•v = 12√2cos 135°

u•v = 12√2× -1/√2

u•v = -12√2/√2

u•v = -12

For the diagram of the vectors, find it in the attachment below.