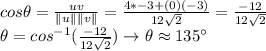Answer:
Check the graph below for the sketch.
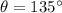
Explanation:
1) Let's organize the data from these Latex codes.
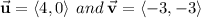
2) Sketching them (Check below). Notice that we are going to use the coordinates of each vector.
3) To find the angle between the vectors, we need to remember the Theorem:
If there is an angle between two vectors a and b, then we can calculate its angle using this relation:
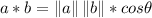
3.1) Then we need the Dot product between u and v. The Dot product is going to give us a scalar value for a product between vectors.
We will also need the norm of each vector. The norm will tell us the length of each one.
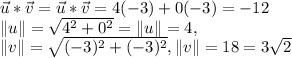
3.2)
Now, we can plug these pieces of information from 3.1 and 3.2 and find the angle: