Answer:
The degrees of freedom are given by:
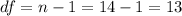
The significance level is
 and then the critical value can be founded in th chi square table we need a quantile that accumulates 0.05 of the area in the right tail of the distribution and for this case is:
and then the critical value can be founded in th chi square table we need a quantile that accumulates 0.05 of the area in the right tail of the distribution and for this case is:
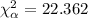
And if the chi square statistic is higher than the critical value we can reject the null hypothesis in favor of the alternative.
Explanation:
We have the followign system of hypothesis:
Null hypothesis:
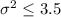
Alternative hypothesis:
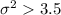
The degrees of freedom are given by:
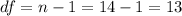
The significance level is
 and then the critical value can be founded in th chi square table we need a quantile that accumulates 0.05 of the area in the right tail of the distribution and for this case is:
and then the critical value can be founded in th chi square table we need a quantile that accumulates 0.05 of the area in the right tail of the distribution and for this case is:
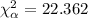
And if the chi square statistic is higher than the critical value we can reject the null hypothesis in favor of the alternative.