Question

Find the critical value of x2 based on the given information H1 >3.5 n=14 a=0.05

Answer 1

The degrees of freedom are given by:

`df = n-1=14-1=13`

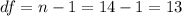
The significance level is
`\alpha=0.05` and then the critical value can be founded in th chi square table we need a quantile that accumulates 0.05 of the area in the right tail of the distribution and for this case is:

`\chi^2_(\alpha)= 22.362`

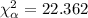
And if the chi square statistic is higher than the critical value we can reject the null hypothesis in favor of the alternative.

Explanation:

We have the followign system of hypothesis:

Null hypothesis:
`\sigma^2 \leq 3.5`

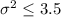
Alternative hypothesis:
`\sigma^2 >3.5`

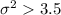
The degrees of freedom are given by:

`df = n-1=14-1=13`

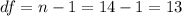
The significance level is
`\alpha=0.05` and then the critical value can be founded in th chi square table we need a quantile that accumulates 0.05 of the area in the right tail of the distribution and for this case is:

`\chi^2_(\alpha)= 22.362`

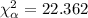
And if the chi square statistic is higher than the critical value we can reject the null hypothesis in favor of the alternative.