Question

11. A vector M is 15.0 cm long and makes an angle of 20° CCW from x axis and another vector N is 8.0 cm long and makes an angle of 40° clockwise from the x axis. Find out resultant vector with its magnitude and direction using components method.

Answer 1

The magnitude of the resultant vector is 22.66 cm and it has a direction of 29.33°

Step-by-step explanation:

To find the resultant vector, you first calculate x and y components of the two vectors M and N. The components of the vectors are calculated by using cos and sin function.

For M vector you obtain:

`M=M_x\hat{i}+M_y\hat{j}\\\\M=15.0cm\ cos(20\°)\hat{i}+15.0cm\ sin(20\°)\hat{j}\\\\M=14.09cm\ \hat{i}+5.13\ \hat{j}`

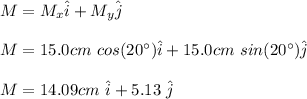
For N vector:

`N=N_x\hat{i}+N_y\hat{j}\\\\N=8.0cm\ cos(40\°)\hat{i}+8.0cm\ sin(40\°)\hat{j}\\\\N=6.12cm\ \hat{i}+5.142\ \hat{j}`

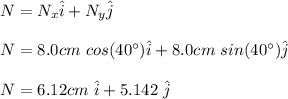
The resultant vector is the sum of the components of M and N:

`F=(M_x+N_x)\hat{i}+(M_y+N_y)\hat{j}\\\\F=(14.09+6.12)cm\ \hat{i}+(5.13+5.142)cm\ \hat{j}\\\\F=20.21cm\ \hat{i}+10.27cm\ \hat{j}`

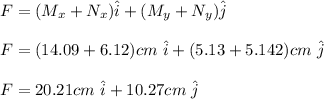
The magnitude of the resultant vector is:

`|F|=√((20.21)^2+(10.27)^2)cm=22.66cm`

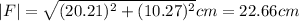
And the direction of the vector is:

`\theta=tan^(-1)((10.27)/(20.21))=29.93\°`

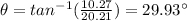
hence, the magnitude of the resultant vector is 22.66 cm and it has a direction of 29.33°