Answer:
The magnitude of the resultant vector is 22.66 cm and it has a direction of 29.33°
Step-by-step explanation:
To find the resultant vector, you first calculate x and y components of the two vectors M and N. The components of the vectors are calculated by using cos and sin function.
For M vector you obtain:
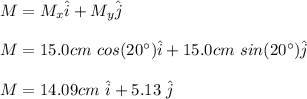
For N vector:
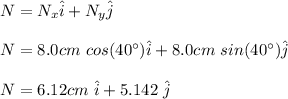
The resultant vector is the sum of the components of M and N:
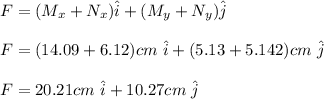
The magnitude of the resultant vector is:
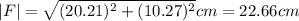
And the direction of the vector is:
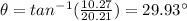
hence, the magnitude of the resultant vector is 22.66 cm and it has a direction of 29.33°