Question

Another type of painted ceramic vessel is called three-circle red-on-white ( Mimbres Mogollon Archaeology). At four different sites in an archaeological region, the number of such sherds was counted in local dwelling excavations.

Site I Site II Site III Site IV
16 19 30 19
25 7 20 24
6 33 10 13
24 2 47 34
14 21 11
15 12
Shall we reject or not reject the claim that there is no difference in the population mean three-circle red-on-white sherd counts for the four sites? Use a 5% level of significance.

Answer 1

Explanation:

Hello!

The objective is to test if the population mean of three-circle red-on-white sheds is equal to the four excavation sites.

To compare the population means you have to apply an ANOVA. For this test the variable of interest is

X: number of three-circle red-on-white sheds.

There is only one factor: "Site" with four treatments "I, II, III; IV"

H₀: μ₁= μ₂= μ₃= μ₄

H₁: At least one population mean is different.

α: 0.05

`F= (MS_(Treatment))/(MS_(Error)) ~~F_(K-1;N-K)`

Df treatments: k-1= 4-1= 3 (k= nº of treatments)

Df errors: N-K= 21-4= 17 (N= total observations for all treatments)

`F_(H_0)= (102.72)/(117.08)= 0.88`

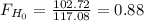
p-value: 0.4723

Using the p-value approach the decision rule is:

p-value ≤ α, reject the null hypothesis.

p-value > α, do not reject the null hypothesis.

The p-value is greater than the level of significance, the decision is to reject the null hypothesis.

Using a 5% significance level, there is not significant evidence to reject the null hypothesis. Then you can conclude that the population mean three-circle red-on-white sherd count is equal to all the excavation sites.

I hope this helps!