Answer:
- Base Length of 84cm
- Height of 42 cm.
Explanation:
Given a box with a square base and an open top which must have a volume of 296352 cubic centimetre. We want to minimize the amount of material used.
Step 1:
Let the side length of the base =x
Let the height of the box =h
Since the box has a square base
Volume,
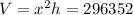
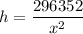
Surface Area of the box = Base Area + Area of 4 sides
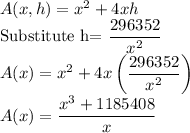
Step 2: Find the derivative of A(x)

Step 3: Set A'(x)=0 and solve for x
![A'(x)=(2x^3-1185408)/(x^2)=0\\2x^3-1185408=0\\2x^3=1185408\\$Divide both sides by 2\\x^3=592704\\$Take the cube root of both sides\\x=\sqrt[3]{592704}\\x=84](https://img.qammunity.org/2021/formulas/mathematics/college/2yt4yl7l5ejcpku8s4p307s9dd2tpj9vah.png)
Step 4: Verify that x=84 is a minimum value
We use the second derivative test
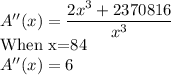
Since the second derivative is positive at x=84, then it is a minimum point.
Recall:
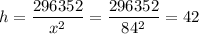
Therefore, the dimensions that minimizes the box surface area are:
- Base Length of 84cm
- Height of 42 cm.