Question

A box with a square base and open top must have a volume of 296352 c m 3 . We wish to find the dimensions of the box that minimize the amount of material used. First, find a formula for the surface area of the box in terms of only x , the length of one side of the square base. [Hint: use the volume formula to express the height of the box in terms of x .] Simplify your formula as much as possible.

Answer 1

• Base Length of 84cm
• Height of 42 cm.

Explanation:

Given a box with a square base and an open top which must have a volume of 296352 cubic centimetre. We want to minimize the amount of material used.

Step 1:

Let the side length of the base =x

Let the height of the box =h

Since the box has a square base

Volume,
`V=x^2h=296352`

`h=(296352)/(x^2)`

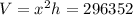
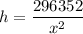
Surface Area of the box = Base Area + Area of 4 sides

`A(x,h)=x^2+4xh\\$Substitute h=(296352)/(x^2)\\A(x)=x^2+4x\left((296352)/(x^2)\right)\\A(x)=(x^3+1185408)/(x)`

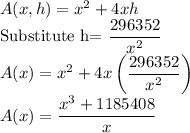
Step 2: Find the derivative of A(x)

`If\:A(x)=(x^3+1185408)/(x)\\A'(x)=(2x^3-1185408)/(x^2)`

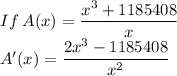
Step 3: Set A'(x)=0 and solve for x

`A'(x)=(2x^3-1185408)/(x^2)=0\\2x^3-1185408=0\\2x^3=1185408\\$Divide both sides by 2\\x^3=592704\\$Take the cube root of both sides\\x=\sqrt[3]{592704}\\x=84`

Step 4: Verify that x=84 is a minimum value

We use the second derivative test

`A''(x)=(2x^3+2370816)/(x^3)\\$When x=84$\\A''(x)=6`

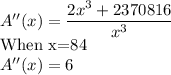
Since the second derivative is positive at x=84, then it is a minimum point.

Recall:

`h=(296352)/(x^2)=(296352)/(84^2)=42`

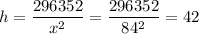
Therefore, the dimensions that minimizes the box surface area are:

• Base Length of 84cm
• Height of 42 cm.