Answer:
(a)
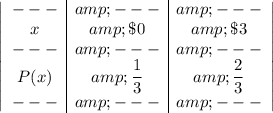
(b)$2
Explanation:
In the given game of rolling a die. these are the possible winnings.
- If the number showing is even(2, 4, or 6) or 1, you win $3.
- If the number showing is either 3 or 5 you win $0.
There are 6 sides in the die.
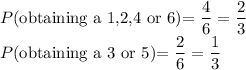
(i)The probability distribution of x.
Let x be the amount won
Therefore:
Probability distribution of x.
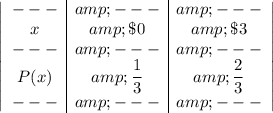
(ii) Expected amount of dollar won
Expected Amount
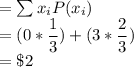
You would expect to win $2.