Question

Let​ T: set of real numbers R Superscript nℝnright arrow→set of real numbers R Superscript mℝm be a linear​ transformation, and let ​{v1​, v2​, v3​} be a linearly dependent set in set of real numbers R Superscript nℝn. Explain why the set ​{T(v1​), ​T(v2​), ​T(v3​)} is linearly dependent.

Answer 1

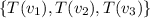`\{T(v_1), T(v_2), T(v_3)\}` is linearly dependent set.

Explanation:

Given:
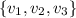`\{v_1,v_2,v_3\}` is a linearly dependent set in set of real numbers R

To show: the set
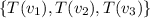`\{T(v_1), T(v_2), T(v_3)\}` is linearly dependent.

Solution:

If
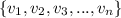`\{v_1,v_2,v_3,...,v_n\}` is a set of linearly dependent vectors then there exists atleast one
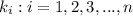`k_i:i=1,2,3,...,n` such that
`k_1v_1+k_2v_2+k_3v_3+...+k_nv_n=0`

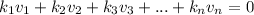
Consider
`k_1T(v_1)+k_2T(v_2)+k_3T(v_3)=0`

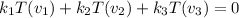
A linear transformation T: U→V satisfies the following properties:

1.
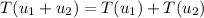
`T(u_1+u_2)=T(u_1)+T(u_2)`

2.
`T(au)=aT(u)`

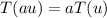
Here,
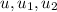`u,u_1,u_2`∈ U

As T is a linear transformation,

`k_1T(v_1)+k_2T(v_2)+k_3T(v_3)=0\\T(k_1v_1)+T(k_2v_2)+T(k_3v_3)=0\\T(k_1v_1+k_2v_2+k_3v_3)=0\\`

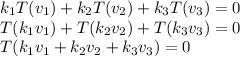
As
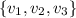`\{v_1,v_2,v_3\}` is a linearly dependent set,

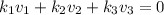`k_1v_1+k_2v_2+k_3v_3=0` for some
`k_i\\eq 0:i=1,2,3`

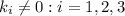
So, for some
`k_i\\eq 0:i=1,2,3`

`k_1T(v_1)+k_2T(v_2)+k_3T(v_3)=0`

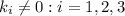
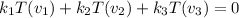
Therefore, set
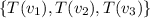`\{T(v_1), T(v_2), T(v_3)\}` is linearly dependent.