Answer:
The relative density = 0.83 which is equivalent to 83%
The degree of saturation, S = 0.58 which gives 58% saturation
Step-by-step explanation:
The parameters given are;
Water content W% = 12%
Bulk unit weight, γ = 18.8 kN/m³
Void ratio of
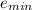 = 0.48
= 0.48
Void ratio of
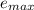 = 0.88
= 0.88
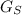 = Constant (As learnt from an answer to the question on the current page) = 2.65 for Sandy soil
= Constant (As learnt from an answer to the question on the current page) = 2.65 for Sandy soil
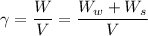
Where, V = 1 m³
W = 18.8 KN
Bulk unit weight, γ =
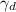 × (1 + W)
× (1 + W)
∴ 18.8 =
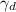 × (1 + 0.12)
× (1 + 0.12)
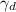 = 18.8/ (1.12) = 16.79 kN/m³
= 18.8/ (1.12) = 16.79 kN/m³
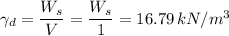
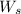 = 16.79 kN
= 16.79 kN
∴
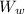 = 18.8 kN - 16.79 kN = 2.01 kN
= 18.8 kN - 16.79 kN = 2.01 kN
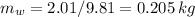
Volume of water = 0.205 m³
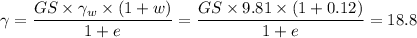
e + 1 = 0.58×GS = 0.58×2.65 =
e = 1.54 - 1 = 0.55
The relative density is given by the relation;
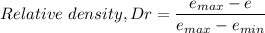
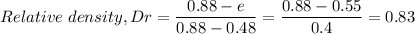
The relative density = 0.83
The relative density in percentage = 0.83×100 = 83%
S·e = GS×w = 0.12·2.65
S×0.55 = 0.318
The degree of saturation, S = 0.58
The degree of saturation, S in percentage = 58%.