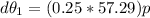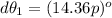Answer:
The maximum possible error of in measurement of the angle is
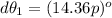
Explanation:
From the question we are told that
The angle of elevation is
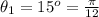
The height of the tree is h
The distance from the base is D
h is mathematically represented as
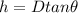 Note : this evaluated using SOHCAHTOA i,e
Note : this evaluated using SOHCAHTOA i,e
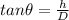
Generally for small angles the series approximation of
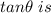
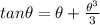
So given that
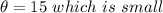
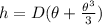
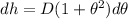
=>
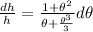
Now from the question the relative error of height should be at most
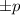 %
%
=>
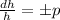
=>
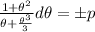
=>
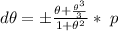
So for
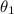
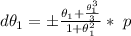
substituting values
![d [(\pi)/(12) ] = \pm ([(\pi)/(12) ] + ([(\pi)/(12) ]^3 )/(3) )/(1+ [(\pi)/(12) ] ^2) * \ p](https://img.qammunity.org/2021/formulas/mathematics/college/pqdmx1nfsnz2z6u4lvgii4vnxeiknxlz4r.png)
=>
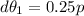
Converting to degree