Question

Can pleasant smells improve​ learning? Researchers timed 21 subjects as they tried to complete​ paper-and-pencil mazes. Each subject attempted a maze both with and without the presence of a floral aroma. Subjects were randomized with respect to whether they did the scented trial first or second. Suppose a paired​ t-test is to be performed to determine whether there is evidence to indicate that the time to complete the maze is faster in scented trials compared to unscented​ trials, on average. For what population can a conclusion be​ made?

Time to complete the maze (seconds)
Unscented 30.2 56.7 51.9 32.2 64.8 42.9 42.7 44.8 25.1 59.2
Scented 25.7 41.9 42.4 34.4 64.7 31.4 40.1 43.2 33.9 40.4
A) Type of Test and Requirements: State the question you are investigating and the type of test that is appropriate for the problem along with the Requirements for the type of test you will be performing. Explain how each of the Requirements are met.
B) Hypotheses: Write the Null and Alternative hypothesis both in words and in symbols.
C) Mechanics: Use the Calculator – include in your answer the type of test, values you entered and your results (test statistic, p-value)
D) Conclusion: State your conclusion (include reject or fail to reject the null hypothesis along with your statement in terms of the problem context and the p-value).
E) Confidence Interval: Find the appropriate (depends upon one or two- tailed test) confidence interval that matches the test and significance level for each problem. Explain how the results of the confidence interval support your hypothesis test conclusion in step 4

Answer 1

a) This is a paired t-test, in which we test the sample of the difference for each pair.

The requirements are:

- The dependant variable must be continous, as we have to calculate the difference. The dependant variable (time) is continous.

- The observations are independent of each other. Although it is not explicitly written, we assumed that the subjects results are independent.

- The dependent variable should be approximately normally distributed. This is assumed.

- The dependent variable should not contain any outliers. No outliers are seen in the data.

b) The null and alternative hypothesis are:

`H_0: \mu_d=0\\\\H_a:\mu_d> 0`

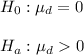
The alternative hypothesis states that the mean difference between the two scenarios is significantly higher than zero.

The null hypothesis states that the mean difference between the two scenarios is not significantly higher than zero.

c) Test statistic t = 1.96

P-value = 0.041

d) As the P-value (0.041) is smaller than the significance level (0.05), the effect is significant.

The null hypothesis is rejected.

There is enough evidence to support the claim that the true difference in the time of the unscented trial and the scented trial is significantly higher than zero.

e) The one-sided upper 95% confidence bound for this example is 0.33 seconds.

As the (lower) bound of the confidence interval is grater than 0, we are 95% confident that the true difference is higher than 0 with 95% confidence.

This is equivalent to the conclusion of the hypothesis test, stating that the true difference is significantly higher than 0.

Explanation:

This is a paired t-test, so the sample we will use to perform the hypothesis test is the difference between the time to complete the mazed in scented trials and unscented trials.

The difference of each subject is:

`d_i=X_(Ui)-X_(Si)`

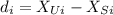
For example, for the first subject, we have:

`d_1=X_(U1)-X_(S1)=30.2-25.7=4.5`

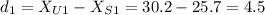
Then, the sample of the difference is [4.5, 14.8, 9.5, -2.2, 0.1, 11.5, 2.6, 1.6, -8.8, 18.8 ].

The sample mean of the difference is:

`M=(1)/(10)\sum_(i=1)^(10)(4.5+14.8+9.5+(-2.2)+0.1+11.5+2.6+1.6+(-8.8)+18.8)\\\\\\ M=(52.4)/(10)=5.2`

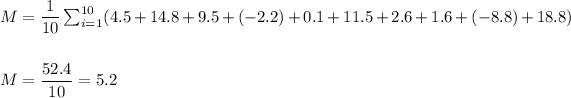
The sample standard deviation is:

`s=\sqrt{(1)/((n-1))\sum_(i=1)^(10)(x_i-M)^2}\\\\\\s=\sqrt{(1)/(9)\cdot [(4.5-(5.2))^2+...+(18.8-(5.2))^2]}\\\\\\ s=\sqrt{(1)/(9)\cdot [(0.548)+...+(183.87)]}\\\\\\s=\sqrt{(632.264)/(9)}=√(70.25)\\\\\\s=8.4`

Now, we can perform hypothesis test for the population difference.

The claim is that the true difference in the time of the unscented trial and the scented trial is significantly higher than zero.

Then, the null and alternative hypothesis are:

`H_0: \mu_d=0\\\\H_a:\mu_d> 0`

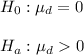
The significance level is 0.05.

The sample has a size n=10.

The sample mean is M=5.2.

As the standard deviation of the population is not known, we estimate it with the sample standard deviation, that has a value of s=8.4.

The estimated standard error of the mean is computed using the formula:

`s_M=(s)/(√(n))=(8.4)/(√(10))=2.66`

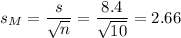
Then, we can calculate the t-statistic as:

`t=(M-\mu)/(s/√(n))=(5.2-0)/(2.66)=(5.2)/(2.66)=1.96`

The degrees of freedom for this sample size are:

`df=n-1=10-1=9`

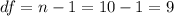
This test is a right-tailed test, with 9 degrees of freedom and t=1.96, so the P-value for this test is calculated as (using a t-table):

`\text{P-value}=P(t>1.96)=0.041`

As the P-value (0.041) is smaller than the significance level (0.05), the effect is significant.

The null hypothesis is rejected.

There is enough evidence to support the claim that the true difference in the time of the unscented trial and the scented trial is significantly higher than zero.

E) We have to calculate a one-side 95% confidence interval for the mean difference.

The population standard deviation is not known, so we have to estimate it from the sample standard deviation and use a t-students distribution to calculate the critical value.

The t-value for a right-tailed 95% confidence interval and 9 degrees of freedom is t=1.83.

The margin of error (MOE) can be calculated as:

`MOE=t\cdot s_M=1.83 \cdot 2.66=4.87`

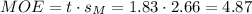
Then, the lower bound of the confidence interval is:

`LL=M-t \cdot s_M = 5.2-4.87=0.33`

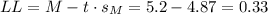
The one-sided upper 95% confidence bound for this example is 0.33 seconds.