Question

Tags are placed to the left leg and right leg of a bear in a forest. Let A1 be the event that the left leg tag is lost and the event that the A2 right leg tag is lost. Suppose these two events are independent and P(A1)=P(A2)=0.4. Find the probability that exactly one tag is lost, given that at least one tag is lost (write it up to second decimal place).

Answer 1

0.75 = 75% probability that exactly one tag is lost, given that at least one tag is lost

Explanation:

Independent events:

If two events, A and B, are independent, then:

`P(A \cap B) = P(A)*P(B)`

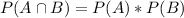
Conditional probability:

`P(B|A) = (P(A \cap B))/(P(A))`

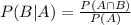
In which

P(B|A) is the probability of event B happening, given that A happened.

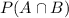`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

In this question:

Event A: At least one tag is lost

Event B: Exactly one tag is lost.

Each tag has a 40% = 0.4 probability of being lost.

Probability of at least one tag is lost:

Either no tags are lost, or at least one is. The sum of the probabilities of these events is 1. Then

`p + P(A) = 1`

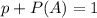
p is the probability none are lost. Each one has a 60% = 0.6 probability of not being lost, and they are independent. So

p = 0.6*0.6 = 0.36

Then

`P(A) = 1 - p = 1 - 0.36 = 0.64`

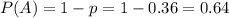
Intersection:

The intersection between at least one lost(A) and exactly one lost(B) is exactly one lost.

Then

Probability at least one lost:

First lost(0.4 probability) and second not lost(0.6 probability)

Or

First not lost(0.6 probability) and second lost(0.4 probability)

So

`P(A \cap B) = 0.4*0.6 + 0.6*0.4 = 0.48`

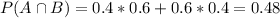
Find the probability that exactly one tag is lost, given that at least one tag is lost (write it up to second decimal place).

`P(B|A) = (0.48)/(0.64) = 0.75`

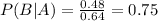
0.75 = 75% probability that exactly one tag is lost, given that at least one tag is lost