Question

You operate a gaming Web site, www.mudbeast.net, where users must pay a small fee to log on. When you charged $3 the demand was 1100 log-ons per month. When you lowered the price to $2.50, the demand increased to 1375 log-ons per month.

A) Construct a linear demand function for your Web site and hence obtain the monthly revenue R as a function of the log-on fee x.
B) Your Internet provider charges you a monthly fee of $30 to maintain your site. Express your monthly profit P as a function of the log-on fee x.
C) Determine the log-on fee you should charge to obtain the largest possible monthly profit. What is the largest possible monthly profit?

Answer 1

A) The linear relation between price and demand is:

`d=-550x+2750`

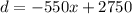
The revenue R is:

`R=-550x^2+2750x`

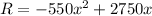
B) The profit functionP is:

`P=-550x^2+2750x-30`

C) The largest monthly profit is obtained with a log-on fee of $2.5 per month. This corresponds to a profit of $3407.5.

Explanation:

We have a site where the number of log-ons depends on our monthly fee. A linear relation is established between the price (log-on fee) and the number of log-ons.

We have two points for this linear relationship:

• At price x=3, the demand is d=1100.
• At price x=2.5, the demand is d=1375.

We will model the relation:

`d=mx+b`

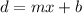
We can calculate the slope m as:

`m=(\Delta d)/(\Delta x)=(d_2-d_1)/(x_2-x_1)=(1375-1100)/(2.5-3)\\\\\\m=(275)/(-0.5)=-550`

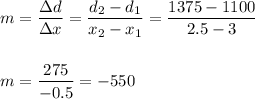
Then, replacing one point in the linear equation, we can calculate the intercept b:

`d_1=mx_1+b\\\\1100=(-550)\cdot 3+b\\\\1100=-1650+b\\\\b=1100+1650=2750`

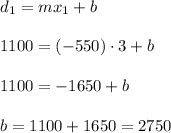
Then, the linear relation between demand and price is:

`d=-550x+2750`

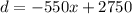
The revenue R can be expressed as the multiplication of the price and the demand:

`R=x\cdot d=x(-550x+2750)=-550x^2+2750x`

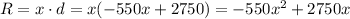
If we have a fixed cost of $30 per month, the profit P is:

`P=R-FC=-550x^2+2750x-30`

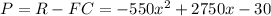
We can maximize the profit by deriving the profit function and making it equal to zero.

`(dP)/(dx)=0\\\\\\(dP)/(dx)=-550(2x)+2750(1)=0\\\\\\-1100x+2750=0\\\\x=(2750)/(1100)=2.5`

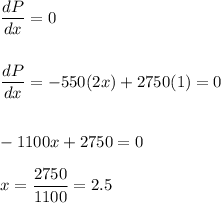
This corresponds to a profit of:

`P(2.5)=-550(2.5)^2+2750(2.5)-30\\\\P(2.5)=-550\cdot 6.25+6875-30\\\\P(2.5)=-3437.5+6875-30\\\\P(2.5)=3407.5`