Answer:
A) The linear relation between price and demand is:
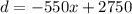
The revenue R is:
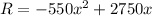
B) The profit functionP is:
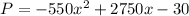
C) The largest monthly profit is obtained with a log-on fee of $2.5 per month. This corresponds to a profit of $3407.5.
Explanation:
We have a site where the number of log-ons depends on our monthly fee. A linear relation is established between the price (log-on fee) and the number of log-ons.
We have two points for this linear relationship:
- At price x=3, the demand is d=1100.
- At price x=2.5, the demand is d=1375.
We will model the relation:
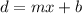
We can calculate the slope m as:
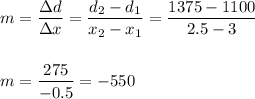
Then, replacing one point in the linear equation, we can calculate the intercept b:
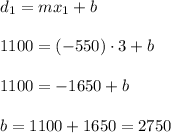
Then, the linear relation between demand and price is:
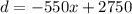
The revenue R can be expressed as the multiplication of the price and the demand:
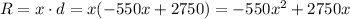
If we have a fixed cost of $30 per month, the profit P is:
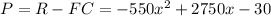
We can maximize the profit by deriving the profit function and making it equal to zero.
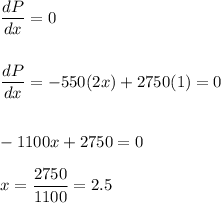
This corresponds to a profit of:
