Question

A shipping pallet holds 10 boxes. Each box holds 300 parts of different

types. The part weight is normally distributed with a mean of 1 lb and a
standard deviation of 0.2 lb.
a. Compute the mean and standard deviation of the pallet weight.b. Compute the probability that the pallet weight will exceed 3015 lb.

Answer 1

(a) The mean and standard deviation of the pallet weight are 3000 lb and 10.95 lb respectively.

(b) The probability that the pallet weight (W) will exceed 3015 lb is 0.085.

Explanation:

Let the random variable X denote the weight of the parts.

The random variable X is normally distributed with parameters, μ = 1 lb and σ = 0.20 lb.

It is provided that a shipping pallet holds 10 boxes and each box holds 300 parts of different types.

That is, there are a total of 300 × 10 = 3000 parts in a pallet.

(a)

Compute the mean and standard deviation of the pallet weight as follows:

Mean of the pallet weight = n × E (X)

`=n*\mu\\\\=3000* 1\\\\=3000`

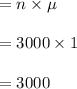
Standard deviation of the pallet weight =
`√(3000* V(X))`

`=\sqrt{3000* (0.20)^(2)}\\\\=√(120)\\\\=10.9544512\\\\\approx10.95`

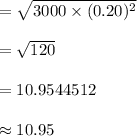
Thus, the mean and standard deviation of the pallet weight are 3000 lb and 10.95 lb respectively.

(b)

Compute the probability that the pallet weight (W) will exceed 3015 lb as follows:

`P(W>3015)=P((W-\mu)/(\sigma)>(3015-3000)/(10.95))`

`=P(Z>1.37)\\\\=1-P(Z<1.37)\\\\=1-0.91466\\\\=0.08534\\\\\approx0.085`

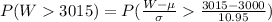
*Use a z-table.

Thus, the probability that the pallet weight (W) will exceed 3015 lb is 0.085.