Answer:
![(dx(t))/(dt) = kx(t)[1000-x(t)],$ x(0)=0](https://img.qammunity.org/2021/formulas/mathematics/college/8z9hpdiace6c9h8wyl04oylj8z61bd10ms.png)
Explanation:
Total Number of People on Campus =1000
Let the number of people who have contracted the flu =x(t)
Therefore, the number of people who have not contracted the flu =1000-x(t)
Since the rate at which the disease spreads is proportional to the number of interactions between the people who have the flu and the number of people who have not yet been exposed to it.
![(dx(t))/(dt) \propto x(t)[1000-x(t)]](https://img.qammunity.org/2021/formulas/mathematics/college/nqovudyo230rl49q6wfdayursl6cjzmxsj.png)
Introducing the proportional constant k, we obtain:
![(dx(t))/(dt) = kx(t)[1000-x(t)]](https://img.qammunity.org/2021/formulas/mathematics/college/x37s3qs8viefj6b9hgjzl7i9yv95dvlebp.png)
At t=0, there was no infected on the campus, therefore the initial condition is given:
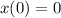
Therefore, a differential equation for the number of people x(t) who have contracted the flu is:
![(dx(t))/(dt) = kx(t)[1000-x(t)],$ x(0)=0](https://img.qammunity.org/2021/formulas/mathematics/college/8z9hpdiace6c9h8wyl04oylj8z61bd10ms.png)