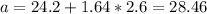Answer:
Percentile 5
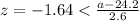
And if we solve for a we got

Percentile 95

And if we solve for a we got
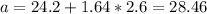
Explanation:
Let X the random variable that represent the variable of interest of a population, and for this case we know the distribution for X is given by:

Where
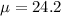 and
and
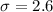
We want to find the percentiles 5 and 95 for this case.
Percentile 5
For this part we want to find a value a, such that we satisfy this condition:
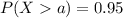 (a)
(a)
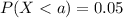 (b)
(b)
We want to find a percentile with 0.95 of the area on the left and 0.05 of the area on the right it's z=-1.64. On this case P(Z<-1.64)=0.05 and P(z>-1.64)=0.05
Using this condition we got:
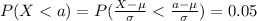
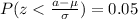
Replacing we got:
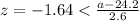
And if we solve for a we got

Percentile 95

And if we solve for a we got