Answer:
The variation rate is 4.07 × 10⁻⁵ cm²/ºC
Explanation:
The relationship of the change in length as a function of the temperature, which are given in this problem can be written by the expression for the area of a rectangle
a = L × W
Differentiating both sides,
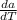 =
=
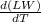
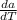 = W
= W
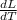 + L
+ L
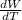
The values they give us are
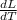 = 1.1 × 10⁻⁵ cm/ºC
= 1.1 × 10⁻⁵ cm/ºC
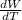 = 8.9 × 10⁻⁶ cm/ºC
= 8.9 × 10⁻⁶ cm/ºC
W = 1.6 cm
L= 2.6 cm
Substituting the values and calculating
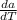 = (1.6 × 1.1 × 10⁻⁵) + (2.6 × 8.9 × 10⁻⁶)
= (1.6 × 1.1 × 10⁻⁵) + (2.6 × 8.9 × 10⁻⁶)
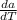 = (1.76 × 10⁻⁵) + (2.31 × 10⁻⁵)
= (1.76 × 10⁻⁵) + (2.31 × 10⁻⁵)
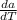 = 4.07 × 10⁻⁵ cm²/ºC
= 4.07 × 10⁻⁵ cm²/ºC
The variation rate is 4.07 × 10⁻⁵ cm²/ºC