Question

The mean and standard deviation for the heights of men in the U.S. are 70 inches and 4 inches respectively and are normally distributed. Based on this information, which of the following represents the percent of men whose heights falls between 58 inches and 66 inches to the nearest whole percent?

A) 2%
B) 16%
C) 34%
D) 68%

Answer 1

B) 16%

Explanation:

First, we need to standardize 58 and 66 inches using the following equation:

`z=(x-m)/(s)`

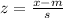
Where m is the mean and s is the standard deviation, so 58 and 66 are equivalent to:

`z=(58-70)/(4)=-3\\z=(66-70)/(4)=-1\\`

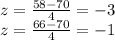
Then, the percent of men whose heights falls between 58 inches and 66 inches is calculated as:

P(58<z<66) = P(-3<z<-1)

So, using the normal table, we get:

P(-3<z<-1) = P(z<-1) - P(z<-3)

P(-3<z<-1) = 0.1587 - 0.0013

P(-3<z<-1) = 0.1574

Finally, 0.1574 rounded to the nearest whole percent is equal to 16%