Question

There is a point $A$ with positive coordinates such that the sum of the coordinates of $A$ is $14$. If the $x$-coordinate of $A$ is $a$, then point $P$ is at $(3a, a^2+13a-11)$. If the slope of a line passing through $A$ and $P$ is $7$, find $a$.

Answer 1

The x-coordinate of A is:

a = 6.1

Explanation:

For point A:

x-coordinate = a

x-coordinate + y-coordinate = 14

y-coordinate = 14 - x-coordinate

y-coordinate = 14 - a

So point A can be written as (a, 14-a)

Let (a,14) be (x₁,y₁)

Point P can be written as (3a, a²+13a-11)

Let P be (x₂,y₂)

Slope of a line passing through 2 point is given as:

`m=(y_2-y_1)/(x_2-x_1)`

where m=7

Substitute all values

`7=((a^2+13a-11)-(14-a))/(3a-a)\\7=(a^2+13a-a-11-14)/(3a-a)\\7=(a^2+12a-25)/(2a)\\14a=a^2+12a-25\\a^2-2a-25=0\\a=6.1,a=-4.1`

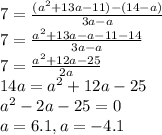
As A has only positive coordinates

a = 6.1