Question

A randomized controlled study was designed to test whether regular drinking of cranberry juice can prevent the recurrence of urinary tract infections (UTIs) in women. 150150 women with a urinary tract infection were treated with an antibiotic and then randomly assigned to one of three groups. One group drank cranberry juice concentrate daily for six months; another group took a drink containing Lactobacillus, a lactose‑fermenting bacterium thought to help inhibit the growth of UTI‑causing bacteria, daily for six months; the last group served as the control group and drank neither cranberry juice nor Lactobacillus drinks for six months. After six months, the number of women in each group with recurring symptomatic urinary tract infection (defined as one or more new infections) was recorded. Here are the results.

Outcome
Treatment Recurring UTI No new UTI Total
Cranberry juice 8 42 50
Lactobacilllus 19 30 49
Control 18 32 50
1. Compute the chi-square statistic, degrees of freedom, and find the p-value for this test.
2. Range of the p-value (to three decimal places): < p-value <

Answer 1

1. The chi-squared statistic = 10.36

The degrees of freedom = 17

The p-value for the test = 0.89

2. The range of the p-value from the Chi squared table = 0.75 < p-value < 0.90

Explanation:

1. The Chi squared test is given as follows;

`\chi ^(2) = \sum (\left (Observed - Expected \right )^(2))/(Expected )`

Therefore,

UTI No UTI % Total

Cranberry juice 8 42 84 50

Lactobacillus 19 30 61 49

Control 18 30 60 50

The chi-squared statistic is given as follows;

`\chi ^(2) = (\left (8- 18\right )^(2))/(18) + (\left (42 - 30\right )^(2))/(30) = 10.36`

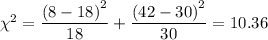
The chi-squared statistic = 10.36

The degrees of freedom, df = 18 - 1 = 17 since the all of the expected count have a minimum value of 18

With the aid of the calculator we find the p value as p as follows;

`p = 0.9 - (10.36 - 10.085)/(12.972 - 10.085) * (0.9 - 0.75)`

The p-value for the test = 0.89

2. The range of the p-value from the Chi squared table is given as follows;

0.75 < p-value < 0.90.