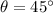Question

The vector wequalsaiplusbj is perpendicular to the line axplusbyequalsc and parallel to the line bxminusayequalsc. It is also true that the acute angle between intersecting lines that do not cross at right angles is the same as the angle determined by vectors that are either normal to the lines or parallel to the lines. Use this information to find the acute angle between the lines below.

a. x + √3y = 1
b. (1 - √3)x + (1 + √3)y = 8

Answer 1

`\theta=45^(\circ)`

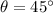
Explanation:

We are given that the equation of lines

`x+\sqrt 3y=1`

`(1-\sqrt 3)x+(1+\sqrt 3)y=8`

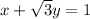
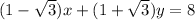
According to question

The vector perpendicular to the lines is given by

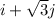`i+\sqrt 3j` and
`(1-\sqrt 3)i+(1+\sqrt 3)j`

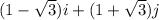
Therefore, the angle between two vectors is given by

`cos\theta=(a_1a_2+b_1b_2)/(√(a^2_1+b^2_1)√(a^2_2+b^2_2))`

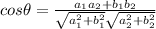
Using the formula

`cos\theta=(1(1-\sqrt 3)+\sqrt 3(1+\sqrt 3))/(2* 2\sqrt 2)`

`cos\theta=(1-\sqrt 3+\sqrt 3+3)/(4\sqrt 2)=(1)/(\sqrt 2)`

`cos\theta=cos 45^(\circ)`

`\theta=45^(\circ)`

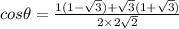
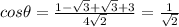
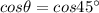
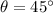
Hence, the acute angle between the lines is given by

`\theta=45^(\circ)`