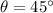Answer:
Explanation:
We are given that the equation of lines
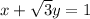
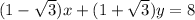
According to question
The vector perpendicular to the lines is given by
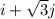 and
and
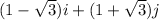
Therefore, the angle between two vectors is given by
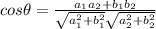
Using the formula
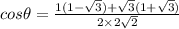
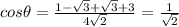
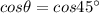
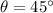
Hence, the acute angle between the lines is given by