Question

A coil 4.15 cm radius, containing 560 turns, is placed in a uniform magnetic field that varies with time according to B=( 1.20×10−2 T/s )t+( 3.40×10−5 T/s4 )t4. The coil is connected to a 530-Ω resistor, and its plane is perpendicular to the magnetic field. You can ignore the resistance of the coil.

(a) Find the magnitude of the induced emf in the coil as a function of time.
(b) What is the current in the resistor at time t = 5.00 s?

Answer 1

(a)
`\epsilon=0.036V+4.119*10^(-4)(T)/(s^4)m^(-2)t^3`

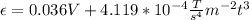
(b) I = 1.65*10^-4 A

Step-by-step explanation:

(a) To find the induced emf in the coil you use the following formula:

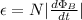`\epsilon=N|(d\Phi_B)/(dt)|` (1)

N: turns = 560

ФB: magnetic flux = AB

A: area = π r^2 = π (0.0415m)^2 = 5.41*10^-3 m^2

you replace the expression for the magnetic flux in the equation (1). Next, you derivative the magnetic field respect to time. Finally, you replace t=5.00s:

`\epsilon=(560)|(d(AB))/(dt)|=(560)(5.41*10^(-3)m^2)|(dB)/(dt)|\\\\B=( 1.20*10^(-2) T/s )t+( 3.40*10^(-5) T/s^4 )t^4\\\\(dB)/(dt)=(1.20*10^(-2)+1.36*10^(-4)T/s^4)t^3(T)/(s)\\\\\epsilon=(560)(5.41*10^(-3)m^2)(1.20*10^(-2)+(1.36*10^(-4)T/s^4)t^3)\\\\\epsilon=(3.029m^2)(1.20*10^(-2)(T)/(s)+(1.36*10^(-4)T/s^4)t^3)\\\\\epsilon=0.036V+4.119*10^(-4)(T)/(s^4)t^3`

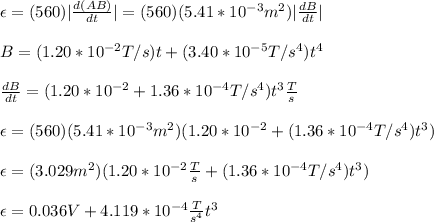
(b) The current is given by:

`I=(\epsilon)/(R)=(0.036V+4.119*10^(-4)T/s^4(5.00s)^3m^(-2))/(530\Omega)\\\\I=1.65*10^(-4)A`