Question

A very long train is rolling at 4 m/s along a straight track. An observer is standing on the ground very dangerously close to the train as moves past notices a person standing on top of a car. When the person on the car is 300 m from the observer, the person begins running toward the observer at 6 m/s.

A. Please write down the velocity vector equation for the person with respect to the ground.
B. How much time does the person take to reach the observer?

Answer 1

A.
`\vec{r}=(6(m)/(s))t\ \ \hat{i}`

B. t = 50 s

Step-by-step explanation:

A. The vectorial equation of the person who is getting closer to the other person is:

`\vec{r}=\vec{v}t`

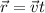
r: position vector

v: speed vector = 6m/s i (if you consider the motion as a horizontal motion)

Then, you replace and obtain:

`\vec{r}=(6(m)/(s))t\ \ \hat{i}`

B. The time is:

`t=(d)/(v)`

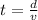
d: distance to the observer = 300m

v: speed of the person on the car = 6.00 m/s

`t=(300m)/(6m/s)=50s`