Question

The production line for Colgate toothpaste is designed to fill tubes with a mean of 6 oz. A sample of 30 tubes will be selected to check the filling process. Assume that the sample had a mean of 6.1 oz and a standard deviation of 0.2 oz. We want to perform a hypothesis test at the 0.05 level of significance to help determine if the filling process should continue or if the machine needs to be corrected. We get the following hypotheses:

H 0 μ = 6 H a μ ≠ 6 We got a P-value of 0.0104. Which of the following is a valid conclusion?
A. There is not sufficient sample evidence to support the claim that the true mean weight, in ounces, of all Colgate toothpaste tubes equals 6 oz.
B. There is sufficient sample evidence to support the claim that the true mean weight, in ounces, of all Colgate toothpaste tubes is not 6 oz.
C. There is not sufficient sample evidence to reject the claim that that the true mean weight, in ounces, of all Colgate toothpaste tubes equals 6 oz.
D. There is sufficient sample evidence to support the claim that the true mean weight, in ounces, of all Colgate toothpaste tubes equals 6 oz.

Answer 1

B. There is sufficient sample evidence to support the claim that the true mean weight, in ounces, of all Colgate toothpaste tubes is not 6 oz.

Explanation:

A two-tailed hypothesis test is performed.

The null and alternative hypothesis are:

`H_0: \mu=6\\\\H_a:\mu\\eq 6`

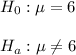
The P-value calculated in this test is 0.0104.

As this P-value (0.0104) is smaller than the significance level (0.05), the effect is significant.

The null hypothesis is rejected.

There is enough evidence to support the claim that the mean fill volume differs significantly from 6 oz.