Answer:
1. 4 days
2. $1.2
3. 1 and 3 gallons
4. 15 and 10
16. 1.2 mi/h
-- Please refer to graph
-- Please refer to graph
Explanation:
Solution 1.
Alex has $40, and Ellen has $24. Alex is saving $6 per day, and Ellen is saving $10 day.
Let x be the number of days in which they both have same money:
As per given statement:
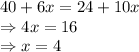
In 4 days, they will have same money.
Solution 2:
Kendra owns a restaurant. She charges $6.00 for two eggs and one piece of toast and $3.60 for one egg and one piece of toast.
Let x be the price of one egg.
Let y be the price of one toast.
As per given statement:
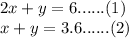
Subtracting (2) from (1):
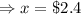
Price of toast = 3.6 - 2.4 = $1.2
Solution 3:
A restaurant has one type of lemonade that is 30% sugar and another that is 10% sugar. Resultant mixture 4 gallons of 15% sugar.
Let x be the amount of lemonade with 30% sugar.
Amount of another lemonade with 10% sugar = (4-x)
As per question statement:
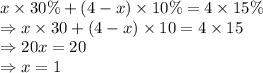
Lemonade with 30% sugar required is 1 gallon.
Lemonade with 10% sugar required is 3 gallons.
Solution 4:
A scientist has a container of 2% acid solution and a container of 5% acid solution. Resultant mixture is 25 fl oz of 3.2%.
Let x be the amount of 2% acid solution.
Amount of another lemonade with 5% acid solution = (25-x)
As per given question statement:
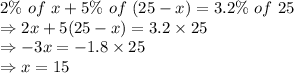
2% acid solution required is 15 fl oz.
5% acid solution required is 10 fl oz.
Solution 16:
Let v be the speed of river current.
Let u be the speed of kayaker.
As per question:
The speed of a kayaker is 5.75 mi/h paddling with the river current and 3.25 mi/h paddling against it.
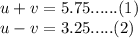
Equation (1) - (2):
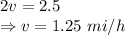
----------------------------------
Susan make $12 per hour babysitting and $24 per hour as a lifeguard. Her goal is to make at least $420.
Let x be the number of hours for babysitting.
Let y be the number of hours as lifeguard.
As per given statement:
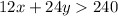
Please refer to graph attached with file name: Inequality
Three possible solutions: (20,20), (21,21) and (22,22)
----------------------------------
25. Joe wants to fence a rectangular pen for his goats. The length of the pen should be at least 40 ft, and the distance around should be no more than 150 ft
Let x be length
and y be width.
As per statement:
x > 40
And perimeter should be less than equal to 240.
2(x+y)
 240
240
Please refer to attached graph with name: "2EquationInq"
Possible dimensions of pen can be (50,20).