Question

Graph the function defined by f(x) = |x+ 2].

Answer 1

Here is the graph:

Hope it helps......!

Answer 2

The graph is a V-shaped curve centered at x =−2.

To graph the function \(f(x) = |x + 2|\), we can follow these steps:

1. **Identify Key Points:**

- The critical point is where
`\(x + 2 = 0\)`, which is
`\(x = -2\)`.

- Choose additional values for \(x\) to plot points on both sides of \(x = -2\).

2. **Evaluate \(f(x)\):**

- Plug the chosen values into the function to find corresponding \(y\) values.

3. **Plot Points:**

- Plot the identified points on the coordinate plane.

4. **Understand the Absolute Value:**

- Remember that
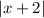`\(|x + 2|\)` is always non-negative.

5. **Draw the Graph:**

- Connect the points with a V-shaped curve.

Let's go through these steps:

1. Choose some values for \(x\):

`- \(x = -5, -3, -2, -1, 0, 2\)`

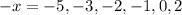
2. Evaluate \(f(x)\):

`- \(f(-5) = |-5 + 2| = 3\)\\ - \(f(-3) = |-3 + 2| = 1\)\\ - \(f(-2) = |-2 + 2| = 0\)\\ - \(f(-1) = |-1 + 2| = 1\)\\ - \(f(0) = |0 + 2| = 2\)\\ - \(f(2) = |2 + 2| = 4\)`

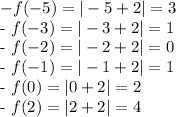
3. Plot Points:

`- \((-5, 3), (-3, 1), (-2, 0), (-1, 1), (0, 2), (2, 4)\)`

4. Draw the Graph:

- Connect the points forming a V-shaped curve.