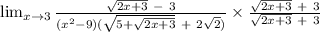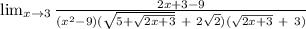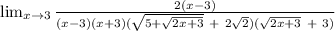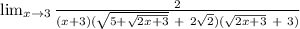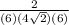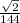Answer:
x = 0 + 2πk
√2 / 144
Explanation:
cos x + cos 2x + cos 3x + cos 4x + cos 5x = 5
Cosine has a maximum of 1, so the only way 5 cosine terms can add up to 5 is if each one equals 1.
cos x = 1 → x = 0 + 2πk
cos 2x = 1 → x = 0 + πk
cos 3x = 1 → x = 0 + ⅔πk
cos 4x = 1 → x = 0 + ½πk
cos 5x = 1 → x = 0 + ⅖πk
The least common multiple of 2, 1, ⅔, ½, and ⅖ is 2.
So the solution that satisfies all five is x = 0 + 2πk.
lim(x→3) [√(5 + √(2x + 3)) − 2√2] / (x² − 9)
To solve without L'Hopital's rule, multiply by the conjugate of the numerator.
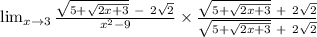
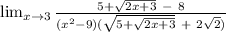
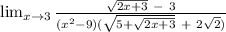
Multiply by the conjugate of the new numerator.