Answer:
Explanation:
To isolate the term of x from one side of the equation, you must multiply by a polynomial.
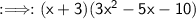
You have to solve with parentheses first.
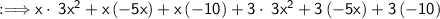
Solve.
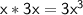
x(-5x)=-5x²
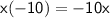
3*3x²=9x²
3(-5x)=-15x
3(-10)=-30
Then, rewrite the problem down.
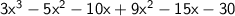
Combine like terms.
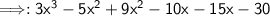
Add/subtract the numbers from left to right.
-5x²+9x²=4x²
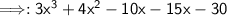
Solve.
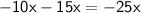
Then rewrite the problem.
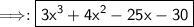
- Therefore, the correct answer is 3x³+4x²-25x-30.
I hope this helps! Let me know if you have any questions.