Question

Calculate the pH of a solution with [H+] = 5.6 x 10^-8

Answer 1

Approximately
`7.25`.

Step-by-step explanation:

If the concentration of
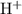`{\rm H^(+)}` ions in a solution is
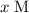`x\; {\rm M}`, the
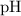`{\rm pH}` of that solution would be
`(-\log_(10)(x))`.

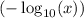Note that the base of the logarithm in this calculation should
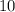`10`. One way to be sure is to state the base explicitly. Using the change of base rule of logarithms:

`\begin{aligned}-\log_(10)(x) = -(\ln(x))/(\ln(10))\end{aligned}`.

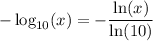In this question, it is implied that the concentration of
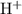`{\rm H^(+)}` in the given solution is
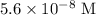`5.6 * 10^(-8)\; {\rm M}`, such that
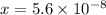`x = 5.6 * 10^(-8)`. Using the equations above:

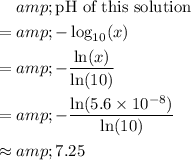`\begin{aligned}& \text{pH of this solution} \\ =\; & -\log_(10)(x) \\ =\; & -(\ln(x))/(\ln(10)) \\ =\; & -(\ln(5.6 * 10^(-8)))/(\ln(10)) \\ \approx\; & 7.25\end{aligned}`.