Question

Whats the minimum and maximum value of f(x)=3(x+8)^2−10

Answer 1

(-8,-10)

Explanation:

Rewrite (x+8)2(x+8)² as (x+8)(x+8).

f(x)=3((x+8)(x+8))−10

Expand (x+8) (x+8) using the FOIL Method.

Apply the distributive property.

f(x)=3(x(x+8)+8(x+8))−10

Apply the distributive property.

f(x)=3(x⋅x+x⋅8+8(x+8))−10
Apply the distributive property.

Simplify and combine like terms.

Simplify each term.

Multiply x by x.

f(x)=3(x2+x⋅8+8x+8⋅8)−10

Move 8 to the left of x.

f(x)=3(x2+8⋅x+8x+8⋅8)−10

Multiply 8 by 8.

f(x)=3(x2+8x+8x+64)−10

Add 8x and 8x.

f(x)=3(x2+16x+64)−10

Apply the distributive property.

f(x)=3x2+3(16x)+3⋅64−10

Simplify.

Multiply 16 by 3.

f(x)=3x2+48x+3⋅64−10

Multiply 3 by 64.

f(x)=3x2+48x+192−10

Subtract 10 from 192.

f(x)=3x2+48x+182

The minimum of a quadratic function occurs at x=
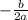`-(b)/(2a)` If a is positive, the minimum value of the function is f (
`-(b)/(2a)`).

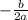Substitute in the values of aa and b.

x=−
`(48)/(2(3))`

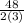
x=-8

Replace the variable x with −8 in the expression.

f(−8)=3(−8)2+48(−8)+182

Y=-10

Therefore, the minimum value is (-8,-10) but if it is asking for just the y-value it would be -10.