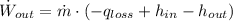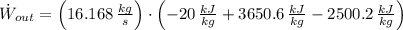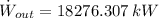Answer:
a)
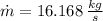 , b)
, b)
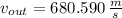 , c)
, c)
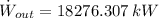
Step-by-step explanation:
A turbine is a steady-state devices which transforms fluid energy into mechanical energy and is modelled after the Principle of Mass Conservation and First Law of Thermodynamics, whose expressions are described hereafter:
Mass Balance
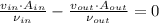
Energy Balance
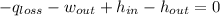
Specific volumes and enthalpies are obtained from property tables for steam:
Inlet (Superheated Steam)
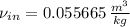
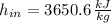
Outlet (Liquid-Vapor Mix)

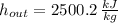
a) The mass flow rate of the steam is:
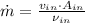
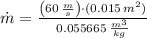
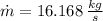
b) The exit velocity of steam is:
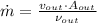
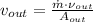
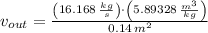
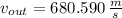
c) The power output of the steam turbine is: