Question

What is the relationship between vectors, complex numbers and polar coordinates? (100 points)

Answer 1

Explanation:

Consider the space
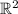`\mathbb{R}^2`. Each point (x,y) can be uniquelly determined by giving values to x and y. The pairs (x,y) in this space can be identified as vectors. In this space identifying a point (x,y) by x and y is using the cartesian coordinates. However, there is anothe way of identifying the point (x,y), which is using polar coordinates. In this coordinates, we identify the point with its distance to the origin (named r) and the angle that makes the line, joining (x,y) and (0,0), with the x axis (named
`\theta`). The way of relating both types of coordinates is given by the equations

`r^2 = x^2+y^2, \theta = \arctan((y)/(x)), x = r\cos(\theta), y = r\sin(\theta)`

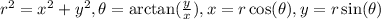
Now, consider a complex number z. They are of the form
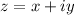`z = x+iy` where x,y are real numbers. In this case, each complex number can be uniquelly described by giving values to x,y. In this case, this is equivalent by considering the cartesian plane, where the y axis is related to the imaginary axis. So, we can uniquelly identify a complex number of the form z = x+iy with a vector in
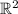`\mathbb{R}^2` of coordinates (x,y). Since in
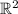`\mathbb{R}^2` we can use polar coordinates, we can use the same coordinates to characterize the complex numbers.