Answer:
The expected number of ticket holders that will fail to show for the flight is 8.34.
Explanation:
For each passenger, there are only two possible outcomes. Either they fail to show up to the flight, or they do not. The probability of a passenger not showing up is independent of other passengers. So we use the binomial probability distribution to solve this question.
Binomial probability distribution
Probability of exactly x sucesses on n repeated trials, with p probability.
The expected value of the binomial distribution is:
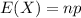
3% of passengers fail to show for flights
This means that
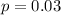
The airline sells 278 tickets
This means that
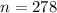
What is the expected number of ticket holders that will fail to show for the flight

The expected number of ticket holders that will fail to show for the flight is 8.34.