Question

Walther owns a home in flood-prone Paradise Basin. If there is no flood the home and land together will be worth $2400. If there is a flood, Walther's home will be destroyed but the land will still be worth $600. There is 1/10 of chance that Walther's house will be destroyed by the flood. Walther can buy flood insurance for $0.2 per dollar of coverage. Let and be the value of respective values of his land in the case of a flood or no flood. Suppose the equation represents the possible values of and that Walther can achieve by buying some amount of insurance. What is the value

Answer 1

$2,554

Step-by-step explanation:

The computation of value is shown below::-

Assume insurance purchase is N units

`C_n_f = Land\ - Flood\ insurance`

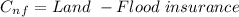
= $2,400 - $0.2 per dollar

`C_f = Land\ worth\ after\ flood - 0.2\ M + M`

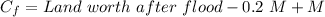
= $600 - 0.2 M + M

= $600 + 0.8 M

`C_n_f = a\ - (C_f)/(b)`

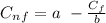
$2,400 - $0.2 M = a - ($600 + 0.8 M) ÷ b

$2,400 - $0.2 M = a - $600 ÷ b - 0.8 ÷ b

now we will equate the situation

-0.2 M = 0.8 M ÷ b

-0.2 = 0.8 ÷ b

b = 4

Now, we will put the value of b to find out the value of a

a - $600 ÷ b = $2,400

a - $600 ÷ 4 = $2,400

a - $150 = $2,400

a = $2,400 + $150

a = $2,550

Now we will find out the a and b by putting the values

= a + b

= $2,550 + 4

= $2,554