Answer:

And solving for t we got:
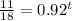
And if we apply natural logs we got:
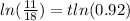
And then the value of t would be:

So then after 5.906 or 6 years we will have approximately 11000 or less for the population
Explanation:
For this case we can use the following model:
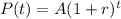
Where A = 18000 the initial value, r = -0.08 since is a decreasing rate and t the number of years. And we want to find the value of t until we have 11000 or lower and we can set up the following equation:

And solving for t we got:
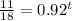
And if we apply natural logs we got:
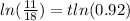
And then the value of t would be:

So then after 5.906 or 6 years we will have approximately 11000 or less for the population