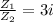Answer:
D) 3 i
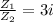
Explanation:
Step(i):-
Given Z₁ = 9 Cis ( 5π/6) = 9 ( Cos (5π/6) +i Sin (5π/6))
Z₂ = 3 Cis ( π/3) = 3 ( Cos (π/3) +i Sin (π/3))
Now Cos (5π/6) = cos (150°) = cos(90°+60°) = -sin 60 =
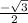
Sin (5π/6) = Sin (150°) = Sin(90°+60°) = Cos 60 =
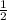
Z₁ = 9 ( Cos (5π/6) +i Sin (5π/6))
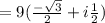
Z₂ = 3 ( Cos (π/3) +i Sin (π/3))
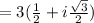
Step(ii):-
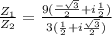
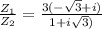
Rationalize with 1 - i √3 and we get
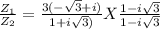
on simplification , we will use formulas
i² = -1 and (a+b)(a-b) = a² - b²
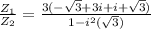
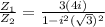
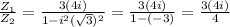
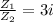
Final answer:-