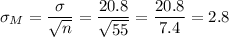Question

There are 572 full-service restaurants in Vermont. The mean number of seats per restaurant is 65.7. [Source: Data based on the 2002 Economic Census from U.S. Census Bureau.] Suppose that the true population mean mu = 65.7 and standard deviation sigma = 20.8 are unknown to the Vermont tourism board. They select a simple random sample of 55 full-service restaurants located within the state to estimate mu. The mean number of seats per restaurant in the sample is M = 69.9, with a sample standard deviation of s = 19.1. The standard deviation of the distribution of sample means (that is, the standard error, sigmaM) is _________ . (Note: Although mu and sigma are unknown to the Vermont tourism board, they are known to you for the purposes of calculating these answers.)

Answer 1

The standard deviation of the distribution of sample means (that is, the standard error, sigmaM) is 2.8.

Explanation:

The standard error, the standard deviation of the sample means, can be calculated as:

`\sigma_M=(\sigma)/(√(n))`

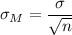
In this case, we know the population standard deviation, so we will use it to calculate the standard error.

If we only know the sample standard deviation, we have to estimate the standard error from the sample standard deviation.

`\sigma_M=(\sigma)/(√(n))=(20.8)/(√(55))=(20.8)/(7.4)=2.8`