Answer:
AC = 36.01
Explanation:
Given ΔABC and ΔADB, since both triangles are right angled triangles then the following are true.
From ΔADB, AB² = AD²+BD²
Given AB = 24 and AD = 16
BD² = AB² - AD²
BD² = 24²-16²
BD² = 576-256
BD² = 320
BD =
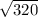
BD = 17.9
from ΔABC, AC² = AB²+BC²
SInce AC = AD+DC and BC² = BD² + DC² (from ΔBDC )we will have;
(AD+DC)² = AB²+ (BD² + DC²)
Given AD = 16, AB = 24 and BD = 17.9, on substituting
(16+DC)² = 24²+17.9²+ DC²
256+32DC+DC² = 24²+17.9²+ DC²
256+32DC = 24²+17.9²
32DC = 24²+17.9² - 256
32DC = 640.41
DC =
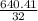
DC = 20.01
Remember that AC = AD+DC
AC = 16+20.01
AC = 36.01