Question

Given: Triangle ABC : triangle ADB. AB =24, AD =16
Find: AC

Answer 1

AC = 36.01

Explanation:

Given ΔABC and ΔADB, since both triangles are right angled triangles then the following are true.

From ΔADB, AB² = AD²+BD²

Given AB = 24 and AD = 16

BD² = AB² - AD²

BD² = 24²-16²

BD² = 576-256

BD² = 320

BD =
`√(320)`

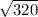
BD = 17.9

from ΔABC, AC² = AB²+BC²

SInce AC = AD+DC and BC² = BD² + DC² (from ΔBDC )we will have;

(AD+DC)² = AB²+ (BD² + DC²)

Given AD = 16, AB = 24 and BD = 17.9, on substituting

(16+DC)² = 24²+17.9²+ DC²

256+32DC+DC² = 24²+17.9²+ DC²

256+32DC = 24²+17.9²

32DC = 24²+17.9² - 256

32DC = 640.41

DC =
`(640.41)/(32)`

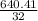
DC = 20.01

Remember that AC = AD+DC

AC = 16+20.01

AC = 36.01