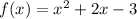Question

Form a quadratic function f(x) for which f(1)=0, f(−1)=−4, and f(2)=5.

Answer 1

`f(x)=x^2+2x-3`

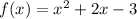
Explanation:

`\textsf{General form of a quadratic function}:f(x)=ax^2+bx+c`

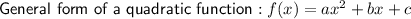
Equation 1

`\begin{aligned}f(1) &=0\\ \implies a(1)^2+b(1)+c &=0\\ a+b+c &=0 \end{aligned}`

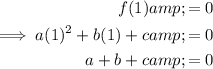
Equation 2

`\begin{aligned}f(-1) &=-4\\ \implies a(-1)^2+b(-1)+c &=-4\\ a-b+c &=-4 \end{aligned}`

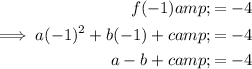
Equation 3

`\begin{aligned}f(2) &=5\\ \implies a(2)^2+b(2)+c &=5\\ 4a+2b+c &=5 \end{aligned}`

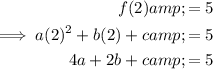
Add Equation 1 and Equation 2:

`\begin{array}{r l}a+b+c & =0 \\+\quad a-b+c & =-4 \\\cline{1-2} 2a+2c & =-4 \end{array}`

`\implies a+c=-2`

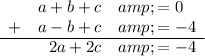
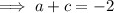
Substitute
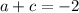`a+c=-2` into Equation 1 and solve for b:

`\begin{aligned}\implies a+b+c &=0\\ b-2 &=0\\ b &=2\end{aligned}`

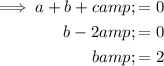
Substitute
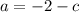`a=-2-c` and
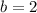`b=2` into Equation 3 and solve for c:

`\begin{aligned} \implies 4a+2b+c&=5\\ 4(-2-c)+2(2)+c &=5\\-8-4c+4+c &=5\\ -3c &=9\\ c &=-3\end{aligned}`

Substitute found value of c into
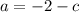`a=-2-c` and solve for a:

`\implies a=-2-(-3)=1`

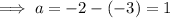
Therefore, a = 1, b = 2 and c = -3

Substitute the found values into the general form of a quadratic function to form the final equation:

`f(x)=x^2+2x-3`