Question

The countries of Europe report that 46% of the labor force is female. The United Nations wonders if the percentage of females in the labor force is the same in the United States. Representatives from the United States Department of Labor plan to check a random sample of over 10,000 employment records on file to estimate the percentage of females in the United States labor force. a) [2 points] They select a random sample of 525 employment records, and find that 226 of the people are females. Obtain a point estimate for the proportion of females in the U.S. labor force. b) [2 points] Compute a 95% confidence interval for the proportion of females in the U.S. labor force. c)[3 points] Interpret your confidence interval from part (b) in context. d)[2 points] Using your confidence interval results from part (b), can we conclude that females make up a majority of the U.S. labor force? Why or why not? Explain your reasoning.

Answer 1

a) Point estimate p=0.43.

b) The 95% confidence interval for the population proportion of female workers in US is (0.388, 0.473).

c) This confidence interval tells us that, with 95% confidence, the true proportion of females in the U.S. labor force is within 0.388 and 0.473.

d) We can conclude that females do not make up a majority of the US labor force, because we can claim, with 95% confidence, that the true proportion of female workers is under 0.473, which is below 0.5 (or 50%).

Explanation:

a) A point estimate can be calculated using the sample results and dividing the amount of female workers in the sample by the sample size:

`p=X/n=226/525=0.43`

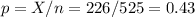
b) We have to calculate a 95% confidence interval for the proportion.

The standard error of the proportion is:

`\sigma_p=\sqrt{(p(1-p))/(n)}=\sqrt{(0.43*0.57)/(525)}\\\\\\ \sigma_p=√(0.000467)=0.022`

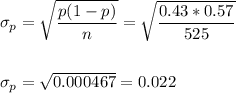
The critical z-value for a 95% confidence interval is z=1.96.

The margin of error (MOE) can be calculated as:

`MOE=z\cdot \sigma_p=1.96 \cdot 0.022=0.042`

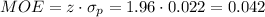
Then, the lower and upper bounds of the confidence interval are:

`LL=p-z \cdot \sigma_p = 0.4305-0.042=0.388\\\\UL=p+z \cdot \sigma_p = 0.4305+0.042=0.473`

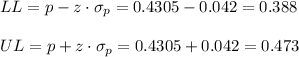
The 95% confidence interval for the population proportion of female workers in US is (0.388, 0.473).

c) This confidence interval tells us that, with 95% confidence, the true proportion of females in the U.S. labor force is within 0.388 and 0.473.

d) We can conclude that females do not make up a majority of the US labor force, because we can claim, with 95% confidence, that the true proportion of female workers is under 0.473, which is below the 50%.

If the confidence interval have included the value 0.5, we could not be sure (with 95% confidence) that female workers do not represent de majority, as there would be possibility that the true proportion is 0.5.