Question

Three potential employees took an aptitude test. Each person took a different version of the test. The scores are reported below. Alissa got a score of 68.568.5; this version has a mean of 60.460.4 and a standard deviation of 99. Morgan got a score of 252.5252.5; this version has a mean of 227227 and a standard deviation of 1717. Norma got a score of 7.967.96; this version has a mean of 6.76.7 and a standard deviation of 0.70.7. If the company has only one position to fill and prefers to fill it with the applicant who performed best on the aptitude test, which of the applicants should be offered the job?

Answer 1

Due to the higher Z-score, Norma should be offered the job

Explanation:

Z-score:

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

In this question:

Whoever has the higher z-score should be offered the job.

Alissa:

`X = 68.5, \mu = 60.4, \sigma = 9`

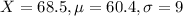
So

`Z = (X - \mu)/(\sigma)`

`Z = (68.5 - 60.4)/(9)`

`Z = 0.9`

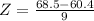
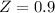
Morgan:

`X = 252.5, \mu = 227, \sigma = 17`

So

`Z = (X - \mu)/(\sigma)`

`Z = (252.5 - 227)/(17)`

`Z = 1.5`

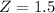
Norma:

`X = 7.96, \mu = 6.7, \sigma = 0.7[tex]</p><p>So</p><p>[tex]Z = (X - \mu)/(\sigma)`

`Z = (7.96 - 6.7)/(0.7)`

`Z = 1.8`

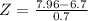
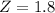
Due to the higher Z-score, Norma should be offered the job