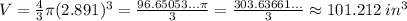Question

The surface area of the sphere is 105 square inches what is the volume of the sphere use 3.14 for pi

Answer 1

The volume of the sphere is
`V\approx101.212 \:in^3`.

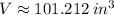Explanation:

A sphere is a 3-D figure in which all of the points in a plane are the same distance from a given point, the center of the sphere.

A sphere with radius r has a volume of

`V=(4)/(3) \pi r^3`

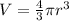
and a surface area of

`S=4\pi r^2`

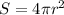
To find the volume of the sphere we use the fact that the surface area of the sphere is 105
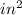`in^2` and we use it to find the radius.

`105=4\pi r^2\\\\4\left(\pi \right)r^2=105\\\\r^2=(105)/(4\pi )\\\\\mathrm{For\:}x^2=f\left(a\right)\mathrm{\:the\:solutions\:are\:}x=√(f\left(a\right)),\:\:-√(f\left(a\right))\\\\r=\sqrt{(105)/(4\pi )},\:r=-\sqrt{(105)/(4\pi )}`

The radius cannot be negative. Therefore,

`r=\sqrt{(105)/(4\pi )}=(√(105)√(\pi ))/(2\pi )\approx 2.891 \:in`

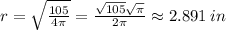
Now, that we know the radius we can find the volume

`V=(4)/(3) \pi (2.891)^3=(96.65053\dots \pi )/(3)=(303.63661\dots )/(3)\approx101.212 \:in^3`