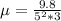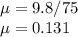Complete Question:
A child is playing in a park on a rotating cylinder of radius, r = 3.00 m , is set in rotation at an angular speed of w = 5.00 rad/s. The base of the cylinder is slowly moved away, leaving the child suspended against the wall in a vertical position. What is the minimum coefficient of friction between the child's clothing and wall needed to prevent it from falling
Answer:
minimum coefficient of friction between the child's clothing and wall needed to prevent it from falling,
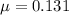
Step-by-step explanation:
Applying the Newton's law:
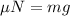 ...............(1)
...............(1)
Where N = Normal reaction.
and
 = coefficient of friction
= coefficient of friction
Since the cylinder is a rotating one, the normal reaction will be calculated using the formula
 .................(2)
.................(2)
Substituting (2) into (1)
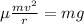 .............(3)
.............(3)
v = wr..........(4)
Substitute (4) into (3)

Substituting, w, g, and r into the equation above
Angular speed,
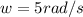
Radius, r = 3 m
g = 9.8 m/s²